Light Scattering
LIGHT
Light and matter: a driving wave and a simple oscillator...
This model for light and matter allows a consistent explanation of a very large part of the subjects which can be included under the general term “Spectroscopy”.
Elastic Scattering is the case where ,e.g., an incoming photon has a particular energy, there is an interaction, the outgoing photon has the same energy.
Elastic scattering is relatively insensitive to the type of atom (with important exceptions), while inelastic scattering where the incoming photon loses energy in the interaction, is very sensitive to the exact nature of the atoms involved and that makes that part of the field of spectroscopy very rich.
Elastic scattering experiments can yield information about the relative orientation and spacing between scatters. Distance and Direction alone in simple cases, with supplemental information (often from a scattering experiment with different conditions) can yield enough information to build a 3D model of these scatterers.
Approach of these lectures is geometric rather than algebraic.
Notation and symbols are still mostly in terms most familiar to crystallographers.
Both geometric and algebraic developments are available in various Crystallography texts.
In other fields, like SAXS, texts seem to mostly do algebraic development of the material.
Study question:
A, B, C live in separate houses inside a fenced area that we cannot get into, but we can move around the edge and throw photons at their houses. From the interference pattern intensities we know that 2 of the houses are 300 ft. north/south of each other, 2 are 400 ft. east:west of each other and 2 are 500 ft. apart in a close-to northwest:southeast direction. At this stage what are the possible layouts of the A,B,C houses?
In addition, From the intensities of scattering one of the houses in both the north:south relationship
and the east:west relationship has more scattering power than the others (big:small scattering is stronger than small:small) and we know that A is indeed the more powerful individual. Now what patterns are possible? What are the relationships of various patterns with each other?
We have evidence that there is some chemistry between A and B that would have them build their houses closer together than to others, then What layouts are possible and What are the relationships of patterns with each other?
The above question presumed that the houses were built on firm land - just as crystals hold objects in position. For a SAXS analogy, If the houses were built on floating island that was randomly spinning around a lot faster than we could make our measurements, then What could be determined about the layout of the houses?
Several different representations and concepts:
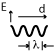
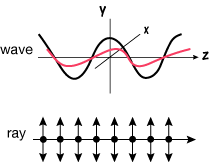
Ray direction of wave propagation, or direction of a beam of photons.
Wave of wavelength λ, each wave broad and long enough to perform as expected.
Photons specific quantum energy ∝ 1/λ, a photon = 1 quantum, a chunk of a wave broad and long enough to perform as expected.
BEWARE: The particle description of a photon is very misleading for scattering/diffraction effects: deflection of balls by other balls or objects is NOT the way photons seem to interact with atoms and produce scattered photons.
Light has both electric and magnetic properties, i.e. electromagnetic wave. One can almost always ignore the magnetic component and still adequately explain experimental phenomena.
Light interacts with matter: The driving wave interacts with an oscillator. Considering the sinusoidally varying electric field of the wave, the oscillator must involve an oscillating dipole, this could be an induced dipole in a polarizable object. So we are getting a measure of polarizability of a medium, e.g., molecules.
Energy can be transfered from (or to) this oscillator, for this introduction we will often ignore most processes except re-radiation of light. (i.e. we can go through an absorption band, but ignore the part that is actual absorption). Absorption is just the loss of energy from the oscillator before it re-radiates. Absorption thus can be thought of as energy lost in the process of getting the oscillator started and keeping it going.
Oscillator (oscillating dipole) can radiate energy (light) So we must consider certain points:
1) Must investigate properties of original interaction
2) Must know character of re-emitted light: is it different from original wave? If so, how?
3) Must investigate how light waves interact with each other since we have opened the possibility of various light waves: e.g. original wave and emitted waves from various oscillators.
For elastic scattering, we will avoid quantum mechanics: except note that any system, including our oscillators, can exist in only certain energy levels; so energy is handled only in discrete chunks which will be important occasionally to consider. But, the picture of a driving wave and a simple oscillator does, in fact, explain much of the observed light scattering phenomena!
Very importantly for us, the model of a driving wave, a simple oscillator, and a scattered wave gives a quantitative description of when and in what directions scattering occurs. This formulation predicts the interference patterns when light is scattered from more than one point, and thus is a functional description of what we observe from an experiment. This works at all wavelengths and all scales, from single atoms and molecules, molecules and other particles in solution, to crystals.
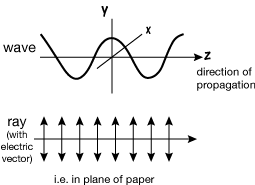
REPRESENTATION OF LIGHT WAVES
Plane polarized light: the simplest case
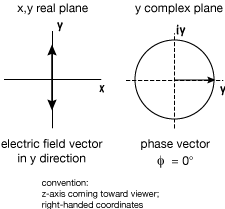

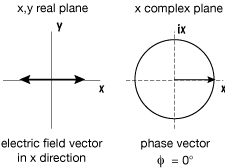
UNPOLARIZED LIGHT
Electric field vectors in all x,y directions
![]()
each component
![]() or
or
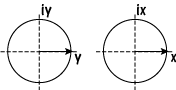
![]() can be treated as composed of x and y
can be treated as composed of x and y
components in phase with each other:
![]()
![]()
The real components add directly
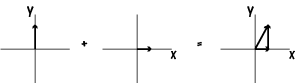
only if φ angle same (i.e. could define φy = φx = 0)
Thus can treat unpolarized light as the resultant of two plane polarized rays in phase. Any arbitrary photon in an unpolarized light ray can be broken into two components, and a great number of photons will then average out to give equal intensities in the two directions of polarized light chosen.
complex planes
 phase vectors φy = φx = 0)
phase vectors φy = φx = 0)
UNPOLARIZED LIGHT SCATTERING FROM A SINGLE PARTICLE
Point Particle (single oscillator)
Straight through:
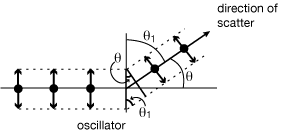
As seen from an angle, i.e. those photons scattered in a particular direction.
For example: direction of scattering in the plane of the paper:
F•scattered = F•original
F↕scattered = F↕original cos(θ)
F↕scattered is a measure of the projection of the dipole motion ⊥ to the direction of scatter.
Ioriginal = F2original
Iscattered = I•scattered + I↕scattered (add components)
Iscattered = F•2scattered + F↕2scattered
The amount of polarization and total Intensity, I = F2, will vary as a function of θ
In the simple case at θ=90°, the ray is completely polarized.
Later we will find that we can describe diffraction as a "reflection" from a plane (a plane of oscillators) and see that this simple 2D diagram works as a projection to explain the general case for crystals.
"X-RAY DIFFRACTION", B. E. Warren, MIT, 1969
Chapter 1 "X-RAY SCATTERING BY ATOMS"
"1.1 CLASSICAL SCATTERING BY A FREE ELECTRON
When an x-ray beam falls on an atom, two processes may occur: (1) the beam may be absorbed with an ejection of electrons from the atom, or (2) the beam may be scattered. We shall first consider the scattering process in terms of classical theory. The primary beam is an electromagnetic wave with electric vector varying sinusoidally with time and directed perpendicular to the direction of propagation of the beam. This electric field exerts forces on the electrons of the atom producing accelerations of the electrons. Following classical electromagnetic theory, an accelerated charge radiates. This radiation, which spreads out in all direction from the atom, has the same frequency as the primary beam, and it is called scattered radiation."
LIGHT AS A WAVE, Interaction of light and matter: plumb bob and ball...
Analogy: Damped Driven Simple Harmonic Motion
Example: bound "electron" and driving "wave" (styrofoam ball on yarn driven by hand wave...)
(or driven by coupled plumb bob for frequency controlled demo.)
Study question:
What is the phase of the ball with respect to plumb bob?
1. plumb bob at length equal to ball-yarn pendulum.
2. plumb bob at length longer than ball-yarn pendulum.
3. plumb bob at length shorter than ball-yarn pendulum.
4. Do-It-Yourself: teach your hand to drive the ball in these three modes...
Study question: plumb bob support provides the coupling. Why does the motion of the supporting beam NOT affect the phase relations?
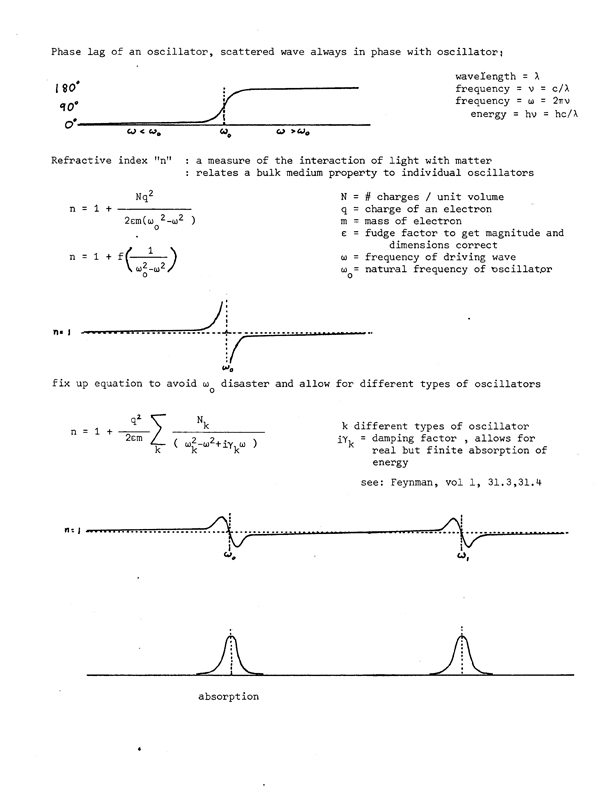
Phase lag of an oscillator, scattered wave always in phase with oscillator:
(Quantum mechanics has its own way of getting broad absorption bands.)
Identify the “oscillators” and we have the field of Absorption Spectroscopy.
LIGHT AS A WAVE, Equation: interaction with oscillator
Points to note:
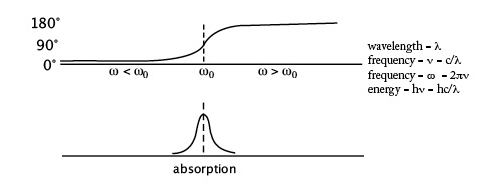
1. Oscillator acts as a radiation source: radiated wave is in phase with the oscillator.
2. The energy that can be pumped into the system, and thus the amount reradiated increases as ω → ω0
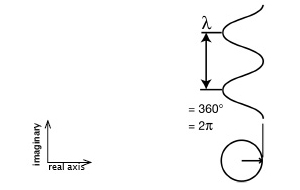
3. For visible light ω < ω0, so oscillator and emitted wave in phase (0°) with the driving wave.
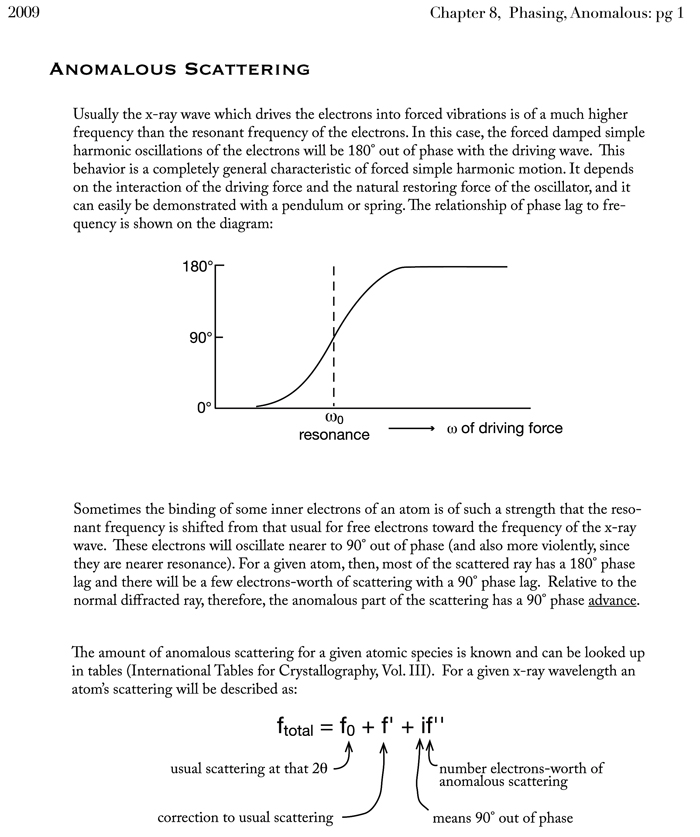
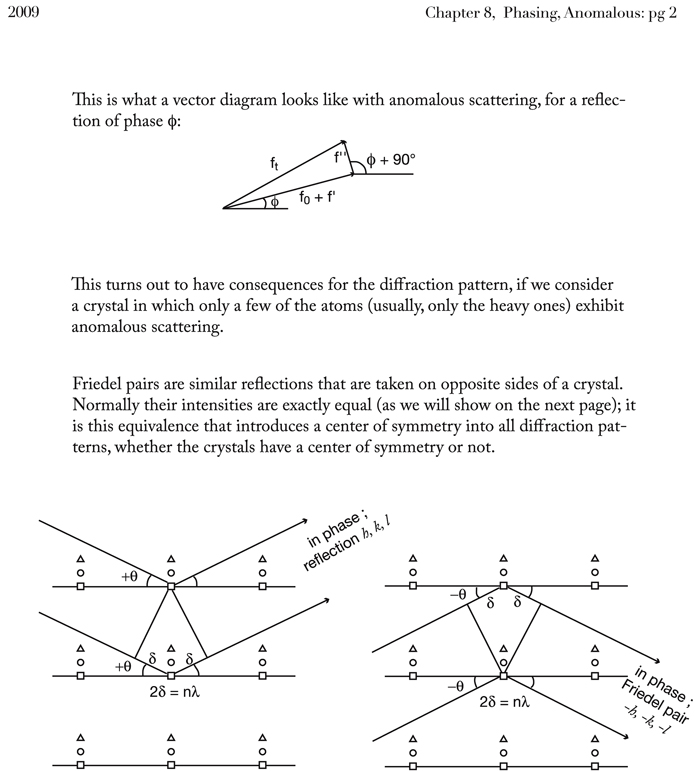
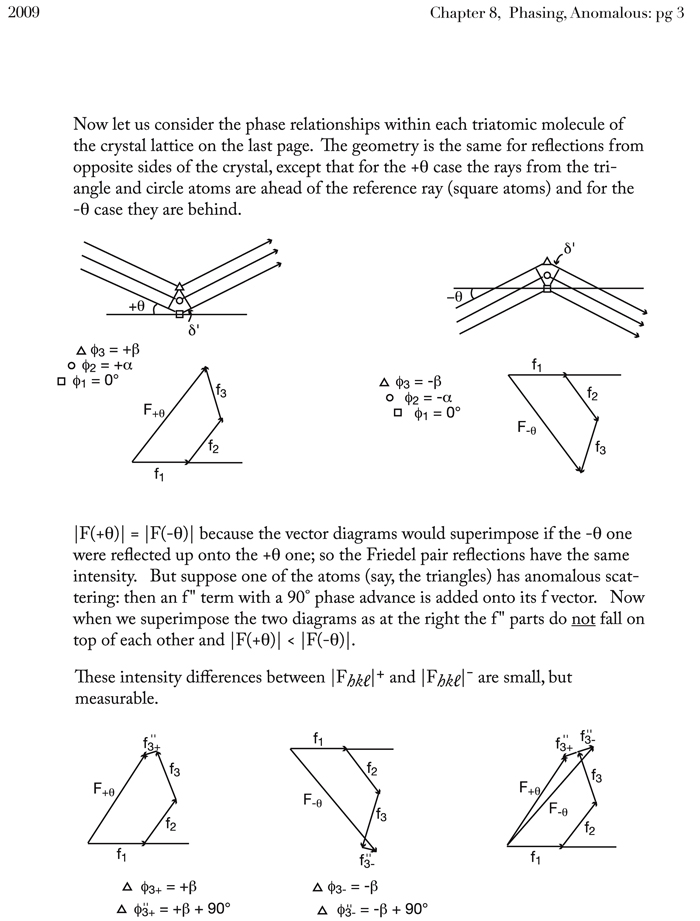
For x-rays ω > ω0 for most electrons in atoms, so oscillator and resulting scattered wave are 180° out of phase with the driving wave. Since one is usually concerned with the scattered wave, this is often defined so that the scattered wave is at 0° and the driving wave at 180°. 4. Usual to treat phase of actual scattered light as having a usual component at 0° and an anomalous component with 90° phase difference (lag). For x-rays with scattered wave redefined to be 0° this is 90°phase advance, see later for a way to draw this).
Simple Harmonic Oscillator, Damped Harmonic Oscillator, Driven Damped Harmonic Oscillator --- put in terms of what it means for light frequency==energy and energy (frequency) of an individual electron.
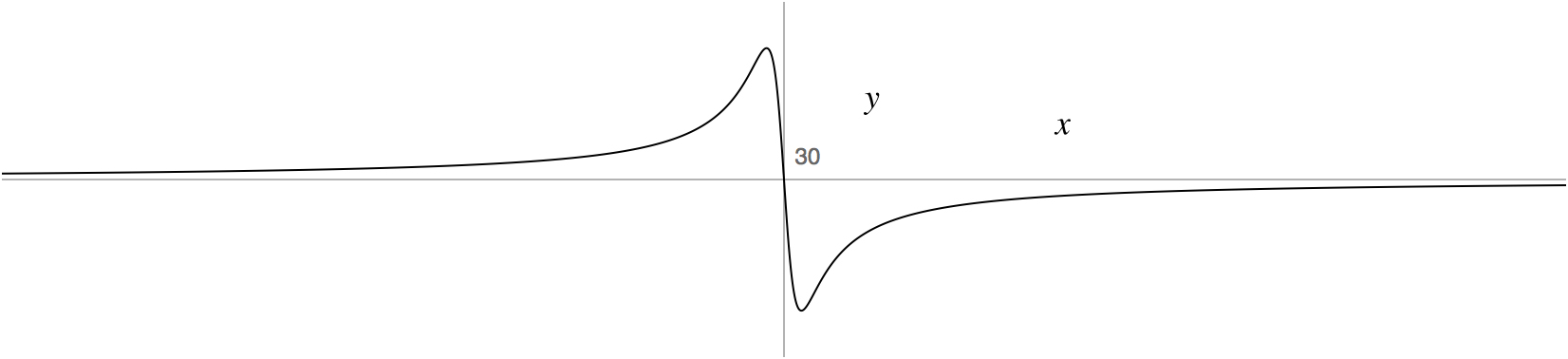
n = refractive index (y axis, arbitrary scale), ω frequency of driving wave (x axis)
n: index of refraction
Describing waves, the phase clock (with radius = amplitude):
(Amplitude factor) • (Phase factor) the general equation of a wave
the expression for a real (light) x-ray, of wavelength set by the real physical experimental conditions.
φ factor (eiφ); eiφ = cos(φ) + isin(φ) exponential form convenient to talk about; cos() & sin() form (real and imaginary components) sometimes more convenient for computation.
Crystallographers use F for Amplitude, crystallography is a major field based on elastic scattering, 2014 is the international year of crystallography, 100 years after the von Laue experiment.
PHASE SHIFT through resonance... Phase lag of an oscillator, scattered wave always in phase with oscillator: (refractive index η is a measure of interaction) η is a measure of the interaction of light with matter: interaction affects relative phase of the oscillator with respect to the driving wave and a probability of feeding energy into the oscillator. The more energy in the oscillator, the more can be lost to other processes like absorption. In any real situation there may be many types of oscillators in the medium interacting with the light but perhaps only one type near enough to resonance to have a significant anomalous scattering component. Also, in common situations almost all of the effective oscillators will have a resonance frequency either greater than the light frequency, as is the case for visible light; or much smaller, as is the case for x-rays. Any odd oscillator which happens to be far on the other side of resonance will make its unique and minor contribution 180° out of phase with the bulk of the scattered radition and thus very slightly diminish the scattered intensity. Wave description works very well for this since its amplitude can be any value and the wave emitted is in all directions from the scatterer - as is observed. REFERENCE PAGES...
Selenium edge: ω0 = 3*1018 sec-1 = .98Å
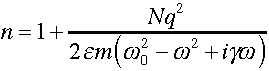
N: Number of charges per unit volume
q: charge of an electron
m: mass of an electron
ε : fudge factor to get magnitude and dimensions correct
ω : frequency of driving wave
γ : damping factor
i : 90° turn from usual, i.e. "imaginary" component
ω0 : natural frequency of oscillator
![]()
However, the description using photons has to account for both its quantized energy and its discret nature - so there has to be a probability of interaction that is the same as the coupling in the wave description and the direction of travel a probability that gives the same energy to the possible directions as given by the wave description. (This gets much more interesting once we consider more than on scatterer!)
Branch to:
2. Molecular Scattering
or: Back to Table of contents
Or continue below into reference material...


HKL2000 demo: usual vs anomalous scattering of elements as a function of wavelength across absorption edges
