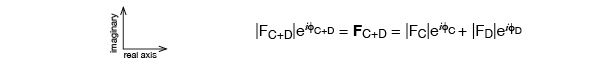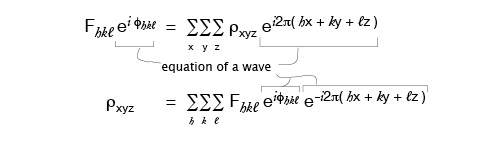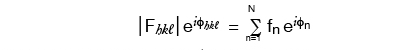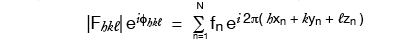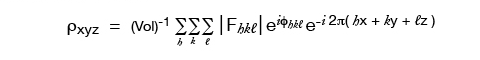SCATTERING OF LIGHT (X-RAYS) BY A MOLECULE
illustrative diagram of an arbitrary SPECIAL CASE
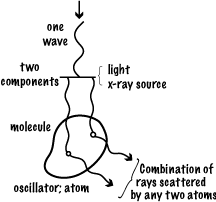
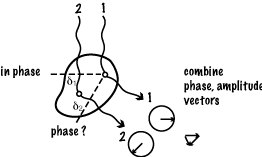
The combination of rays scattered by any two (or more) atoms depends on the amplitude and phase of each scattered ray. The amplitude depends on the [oscillator strength | number of electrons] in that atom (since it is electrons that scatter x-rays). The relative phase of the rays depends on the relative path lengths they have travelled. Wave 2 travels (δ1 + δ2) further than wave 1, so the phase change in that length is (δ1 + δ2)/λ .
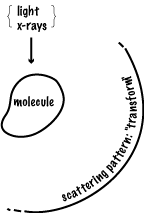
Intensity in any particular direction is a function of the [strength of the oscillators | number of electrons in the atoms] and of their relative positions. So if the molecules were randomly positioned, e.g. by free rotation, one could only find out some general property concerning distance such as how big the diameter (radius of gyration) is of the region where the oscillators are distributed. e.g. low angle x-ray scattering, light scattering experiments. This is of mathematical interest only, unless we can relate the pattern seen (or imagined) here to the pattern of structure in the molecule.
For x-rays the scattered ray has 180° phase shift from the incident ray - but this is true for all scattered rays so it makes no difference to how they combine.
The scattering pattern of a single object is distributed in all directions, and varies fairly smoothly.
COMBINATION OF [X-RAY : LIGHT] WAVES
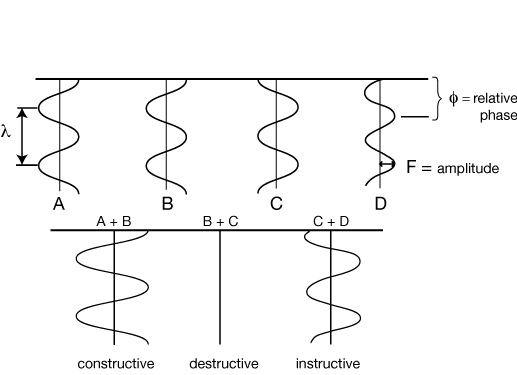
Waves A and B are exactly in phase with one another, and they combine constructively to give a wave of twice their amplitude.
Waves B and C are exactly out of phase, and they cancel completely, combining to give a wave of zero amplitude.
Waves C and D are somewhat out of phase, and they combine to give a wave with an intermediate phase and less than twice their original amplitude.
VECTOR NOTATION FOR WAVES
The length of the vector represents the amplitude of the wave, and the direction of the vector represents the phase of the wave.
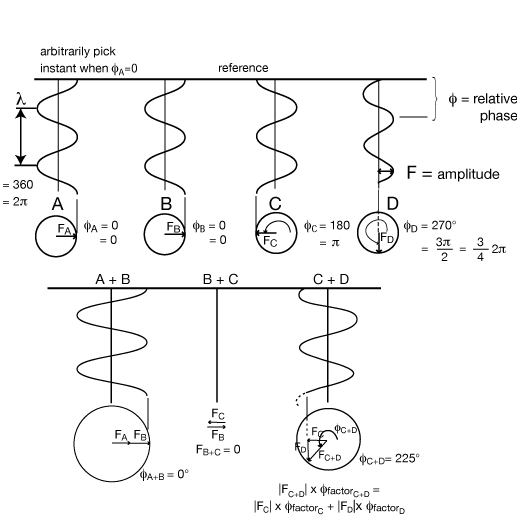
The construction of adding the two vectors head to tail gives the correct amplitude and phase for the combined wave, as above. These are just vectors in the complex plane and can be written as:
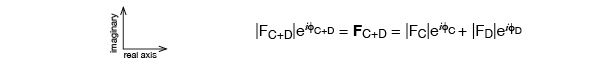
φ factor (eiφ); eiφ = cos(φ) + isin(φ)
SCATTERING FROM 2 OSCILLATORS IN A PLANE

SCATTERING FROM MULTIPLE OSCILLATORS: GENERAL CASE
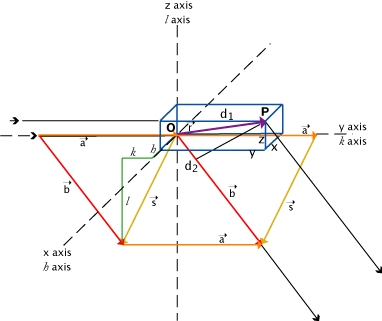
Rule:
h ⊥ y, z
k ⊥ x, z
l ⊥ x, y
If x,y,z orthogonal,
then h,k,l directions
coincident with x,y,z
Point P is an oscillator
O is an arbitrary origin, which may or may not be an oscillator
r is the vector from O to P, with components x, y, z
a and b are standard vectors in the directions of the incident and scattered rays: s = b - a
a, b scaled from unit vectors by 1/λ ; so all these related dimensions will be in Å-1 and express distance as fractions of wavelength.
Path length difference δ = d2 - d1 where,
d1 is projection of r on a direction : d1 = r • a
d2 is projection of r on b direction : d2 = r • b
So, δ = d2 - d1 = r • b - r • a = r • ( b - a ) = r • s
d1 and d2 are unitless as is δ. i.e. δ = δ'/λ where δ' is the real measurement in Å and λ is wavelength in Å so δ is unitless fractional length in terms of wavelength.
δ = r • s
(components): x, y, z • h, k, l (dot product) = hx + ky + lz
δ is dimensionless and x, y, z are in Å; h, k, l are therefore in Å-1 (reciprocal Å): they give us a convenient way of describing a scattered ray.
Relative phase φ = 2π ( hx + ky + lz ) as in |F|eiφ = |F| ei2π( hx + ky + lz ) , expression for a light ray scattered from P.
In this general case h, k, l are not constrained to be integers.
General Equation, simplest form:
Fhkl = |Fhkl| eiφhkl = ∑n fn ei2π(hx + ky + lz)
fn :scattering power of atom n at given λ and scattering angle.
Special Case redrawn with general case vectors:
For any scattering direction b the set of three vectors a, b, s make a triangle, so we can draw the scattering diagram conveniently in the plane of our paper or screen. In the general case of scattering from a single object even though it can contain many scattering points (atoms), the h,k,l of the scattering vector s are not constrained to be integers.
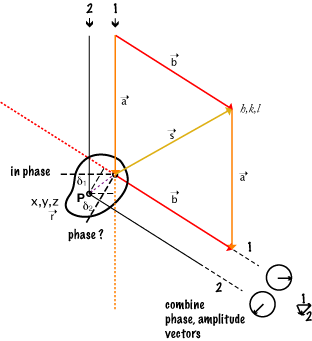
NOTE that the a, b, s relationship is NOT dependent on the location of scattering point P.
Since a and b are "unit" vectors, the magnitude and direction of s is set by the angle of b (the direction in which the scattered ray is observed) to a (the direction of the incident ray).
Download:
 PS-2-interPlanePhases.pdf(120KB)
Problem for this section
PS-2-interPlanePhases.pdf(120KB)
Problem for this section
A point to come back to...
The vector s can be considered as the normal to a set of planes of spacing d which is proportional to 1/|s|. d then can be thought of as a mark on a "Molecular Ruler" normal to those planes such that if two scattering points were separated in that direction by d, then their scattering would be in phase for that s described direction; i.e. for the rays scattered at the angle b makes to a. This point is implied in the math, and can be appreciated by carefully thinking about relative phase, but is much easier to see geometrically for the case where molecules are arranged in a crystal lattice!
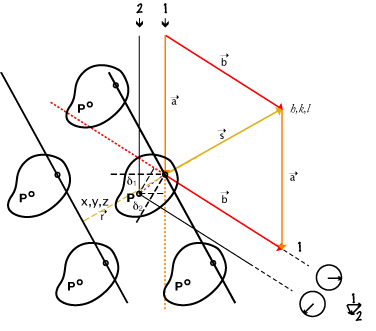
More wresting with units, dimensions:
We need δ = r • s as unitless fractions of wavelength,
so components: x, y, z • h, k, l must multiply to cancel units:
if x, y, z are in Å; then h, k, l in reciprocal Å,: and
if x, y, z are in fractions of something; then h, k, l in related reciprocal fractions.
(Macromolecular coordinates are standardly given in Å.
Spacing in a crystal is traditionally in fractions of a unit cell.)
The pair: Real Space -- Reciprocal Space is a "dual"
There are definable ways, and general mathematical rules, to transform from one set of such coordinate systems to the other. For crystals, the algebra is relatively straight forward to figure out, though a bit tedious for those with non-orthogonal coordinate systems.
The equations we use for this imply repeating functions:
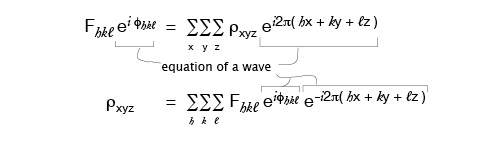
So the idea of a box around the molecule of interest in which we map ρxyz is not only a convenient enclosure, it can be thought of as one box of many identical ones, i.e., a repeating function, a crystal. Each such box would then be called a unit cell.
If we express x, y, z as fractional coordinates in terms of the box dimensions, then h, k, l must be in terms of reciprocal fractions relating to the box dimensions.
If the data is in terms of unitless h, k, l we can get back to the molecule in terms of unitless x, y, z. We would need to know the wavelength to predict where the scattered rays would appear in our experiment, and to get the size of the box in real dimensions for describing the distances between atoms in real dimensions.
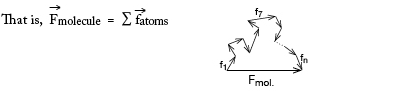
SCATTERING FROM A MOLECULE OF MULTIPLE-ATOMS USING VECTOR NOTATION

Intensity in any given direction (if molecule is in a crystal then only the directions given by the Bragg Law are allowed) is a function of the number of electrons in the atoms (oscillators) and the relative positions of the atoms.
Let h, k, l index the direction of the diffracted (scattered) rays (reflections).
By definition, Intensity = (Amplitude)2 or I = F2 and | Fhkl | = √Ihkl
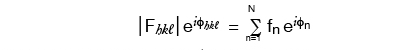
Where fn is the scattering power of the nth atom (oscillator), and
φn is the phase of the ray scattered by the nth atom
(φn is a function of the x,y,z coordinates of that atom)
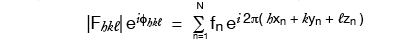
If we knew or guessed all the atom positions we could calculate |F| and φ and so could check a trial structure against the real one by comparing |Fcalculated| vs |Fobserved| for each diffracted ray (reflection). But protein molecules have too many atoms for which to guess positions!
NB: actually fn is dependent on θ, the scattering angle because of polarization effect, size of atom, etc.
HOW AN INDIVIDUAL ATOM AFFECTS THE STRUCTURE FACTOR
- f, the atomic scattering factor:
Atoms (i.e., the distribution of electrons) have a real, finite size, and so it is possible for various parts of an atom to scatter out of phase with one another. The same sort of path-Iength arguments apply as when we considered two separate atoms scattering out of phase. But for a given atom, the electron distribution is approximately spherically symmetric, and the contribution of this factor can be calculated as a function of θ or looked up in tables.

- the B factor :
All uncertainties in the position of an atom is put into the B factor. Thermal motion is only a minor part of the B-factor for atoms of a macromolecule. Atoms seem to vibrate, so their effective scattering is spread over a larger volume. (It may not be a spherically symmetric volume, such as when vibration is along the direction of a bond.) This effect is also a function of θ.
The most common formula for the nth atom (spherically symmetric case) is:
fn,θ e-Bn(sin2θ)/λ2
EQUATIONS AND THE FOURIER TRANSFORM RELATIONSHIP
The Fourier transform is a general concept applicable to all kinds of light scattering, but it really comes into its own with x-ray crystallography where there is sufficient information to apply the details of the equations in a very simple and direct way.
Since it is electrons that are scattering x-rays, the scattering factor can be thought of in terms of the electron density, ρ, throughout the molecule. Rewriting the formula from the previous page in terms of ρ:

where the sum is over a volume that contains the scattering points, for a crystal this is the entire unit cell. So the Volume in these equations is a scaling number but calling it the volume of the repeating unit is a provincialism.
The F’s are the Fourier transform of the electron density, and it conveniently happens to be true that the inverse relation also holds:
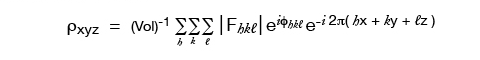
where in theory, but not in practice, the h, k, l sums are from -∞ to +∞.
So the electron density (which is our desired final result) is the Fourier transform of the F’s. Everything on the right-hand side of the equation is known except, still, for φhkl !
We assume that the molecule stays still, oriented in a definite position. For stationary molecules in a crystal, one must consider the consequences of a regular array. (e.g. crystal diffraction)
If however, the molecules tumble in solution, then one must average over all positions.
e.g. Small Angle X-ray Scattering, SAXS.
UNPOLARIZED LIGHT SCATTERING FROM A SINGLE OBJECT (tumbling in space)
GENERAL CASE: single object tumbling in solution: polarization effect
An important but completely predictable common feature.
For scattering from discrete objects tumbling in solution we would need to consider the general case of scattering in all directions.
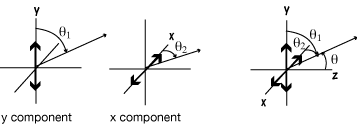
Scattering of Io unpolarized = scattering components 0.5 Io(x) + 0.5 Io(y),
equivalent but for different effective polarization
so one has intensity = 0.5 Iosin2θ1; and the other has Intensity = 0.5 Iosin2θ2.
Thus: Itotal scattered = Ix + Iy = 0.5 Io(sin2θ1 + sin2θ2)
= 0.5 Io(1 + cos2θ)
This describes Intensity in any one direction (i.e. for a particular solid angle)
Field strength = Amplitude per unit area (on a sphere at distance r) decreases as 1/r
Intensity per unit area decreases as 1/r2
This is important since measuring scatter from isolated objects the 1/r term is needed to match observed scatter at the measuring device. (Note that for scattering from a crystal the allowed direction of scatter is limited and the measuring device can capture all the light scattered in a particular direction, so there is not a fall-off of intensity just due to radial spread.)
Now we have some of the geometrical terms in the equation for light scattering from
particles whose diameter is << λ ; i.e., where we can treat the particle as a single oscillator.
In practice that diameter is : d < λ/20.
Small Angle X-ray Scattering (SAXS)
Solution scattering gets especially interesting when the wavelength of the light is of the same length as features within the tumbling molecule, i.e. just the same relations that make crystal scattering really useful for detailed structure determination. In addition to the Intensity equations above, must be added intensity scattered from features within the molecules averaged by tumbling. Rather than building a model into the image obtained from crystallography, the best that can be done is to propose shapes for the molecule and see if the data is consistent with what would be observed from such shapes tumbling in solution. Of course, if one already knows a great deal about the possible structures that a particular molecule might have, like opening/closing between subunits, or donuts around DNA, then the models can be quite detailed. Later, we will derive the general scattering equation - though the crystallographer does not have to describe the tumble averaging.
Match of wavelength to features we want to see:
x-ray: ~1 Å, atom: ~3Å, protein molecule: ~50Å, (bonded atoms: 1.5Å apart)
Green light: 5000 Å, scale to 5meters = 5000 mm , scaled protein: 50mm = 5cm, (bonded atoms: 1.5 mm)
→ Draw 1 wavelength across both boards (e.g. of 147 Nanaline Duke bldg.),
(Note change of phase along wave)
look at two 5 cm patchs "molecules": (or two neighboring 3mm patches "atoms"), myoglobin would be about 5cm in diameter.
even if they would scatter this light, could we tell we had two of them?
5 meters scaled green light wave with scaled molecule; expanded to
32 cycles of 1.5Å across the diameter of myoglobin:
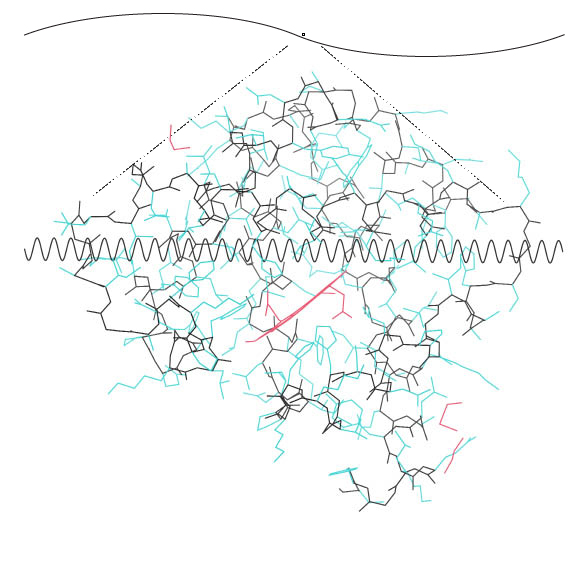
Show here Myoglobin 0.9Å structure with electron density
→ 2NRL.kin with 2nrl.omap in KiNG
 myoglobin 2NRL.kin(3.2MB)
myoglobin 2NRL.kin(3.2MB)
 myoglobin 2nrl.omap(2.2MB)
myoglobin 2nrl.omap(2.2MB)
Note that the atoms are almost resolved, and that the wave length is approximately the length of an atom-atom bond. This structure had data to 0.91 Å resolution. X-rays of 1.5 Å wavelength can possible resolve things spaced as closely as 1.5/2 = .75 Å.
REFERENCE PAGES...
Visible Light Scattering: the sky is blue, clouds are white
ancient hand written notes of step-by-step equations with dimensional analysis and comments.