Tight turns (also known as reverse turns, β turns, β bends, hairpin bends, 310 bends, kinks, widgets, etc.) are the first and most prevalent type of nonrepetitive structure that has been recognized. While helices and β structure have the property that approximately the same φ,ψ angles are repeated for successive residues, pieces of nonrepetitive structure have a particular succession of different φ,ψ values for each residue, so that the concept of residue position within the structure is more influential than in a repeating structure. Of course, no startlingly new local conformations are available: most residues are either approximately α type or β type, with occasional left-handed α-type residues which are usually but not always glycines. However, by combining those three basic conformations in various orders, allowing for the considerable variation available within each of the conformational minima, and utilizing various patterns of hydrogen bonding and side chain position, an enormous number of quite different structures are possible even within a stretch as short as three or four residues.
Tight turns were first recognized from a theoretical conformational analysis by Venkatachalam (). He considered what conformations were available to a system of three linked peptide units (or four successive residues) that could be stabilized by a backbone hydrogen bond between the CO of residue n and the NH of residue n + 3.
He found three general types, one of which (type III) actually has repeating φ,ψ values of -60°, -30° and is identical with the 310-helix. The other two types are nonhelical and fold the chain back on itself around a rather square corner so that the first and fourth α-carbons are only about 5 Å apart, as seen in Fig. 30. The backbone at either end of type I or II turns is in approximately the right position to continue in an antiparallel β ribbon. Type I turns have approximately φ2 = -60°, ψ2 = -30°, φ3 = -90°, ψ3 = 0°, and type II approximately φ2 = -60°, ψ2 = 120°, φ3 = +90°, ψ3 = 0°; these two types are related to one another by a 180° flip of the central peptide unit. Types I and III are identical for residue 2 and differ by only 30° in φ3 and ψ3 (compare Fig. 31a and c).
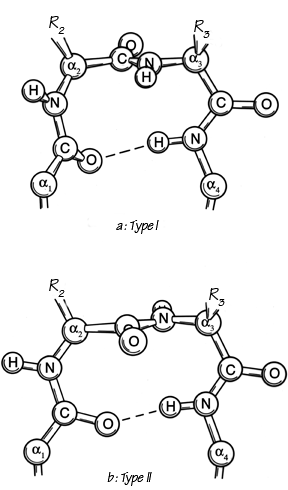
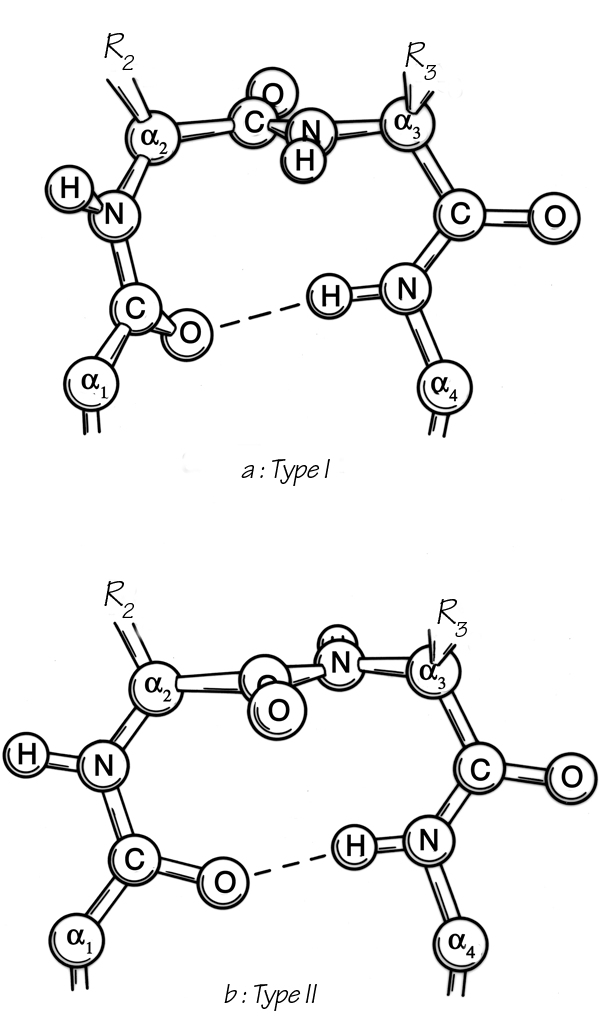
FIG. 30. The two major types of tight turn (I and II). In type II (bottom), R3 is generally glycine.
Types I′ and II′ (see Figs. 31 and 32) are the mirror images (for backbone conformation) of types I and II, with the inverse φ,ψ values of those given above. For types II, II′, and I′ the dihedral angles are such that for one or both of the central positions glycine is strongly preferred. In the rather common type II turn, for instance, the carbonyl oxygen of the middle peptide is too close to the β-carbon of the side chain in position 3 (see Fig. 30b), but the bump is relieved if residue 3 is glycine. For type II′ the bump is between Cβ of residue 2 and the NH of the middle peptide. A survey by Chou and Fasman () that identified and characterized 459 tight turns in actual protein structures found that 61% of the type II turns had a glycine in position 3. Type II′ turns strongly prefer glycine in position 2; types I′ and III′ prefer glycine in position 2, but in the actual cases observed seem to adjust conformation slightly rather than have glycine in position 3.
[Sibanda and Thornton () noticed that tight turns in the classic position joining a β hairpin very strongly preferred the mirror-image I′ and II′ conformations. The otherwise-commonest Type I turn has a very pronounced lefthanded twist (diagnosed by a +45° dihedral angle of the 4 turn Cα's), which is in conflict with the righthanded twist of β strands, while the -45° dihedral of Type I′ matches the twist of a β hairpin almost perfectly. Tight turns joining the strands of a β hairpin, therefore, usually use one or two glycines.]
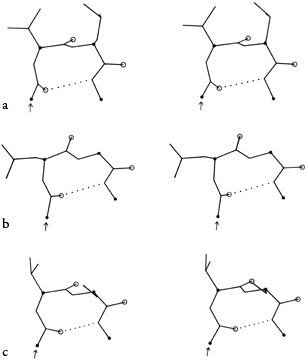
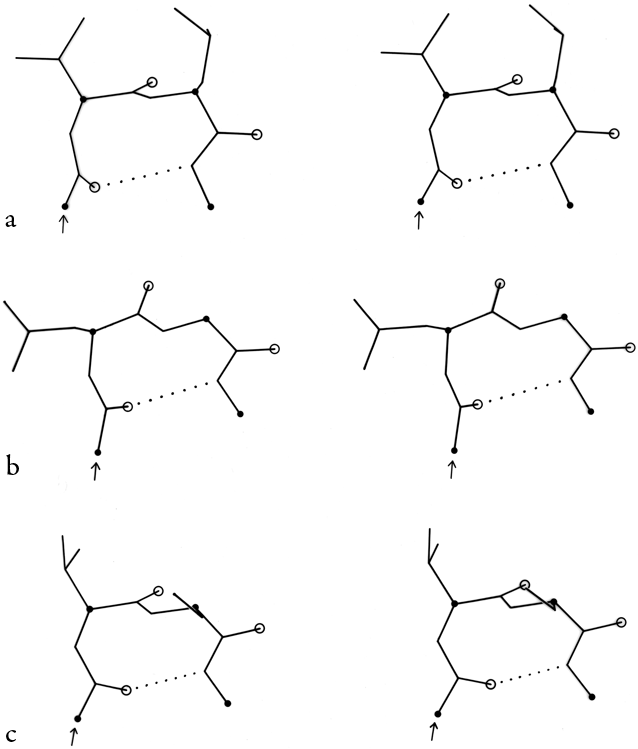
FIG. 31. Stereo drawings of particular examples of type I (a), I′ (b), and III (c) turns from the known protein structures. (a) Thermolysin 12-15 (Gly-Val-Leu-Gly); (b) papain 183-186 (Glu-Asn-Gly-Tyr); (c) flavodoxin 34-37 (Asn-Val-Ser-Asp).
In addition to the above three turn types and their mirror images, Lewis et al. () defined five additional types which both they and Chou and Fasman () find can account for all observed cases (outside of helix) where the α-carbons of residues n and n + 3 are less than 7 Å apart. Type V is a rather unusual departure from type II which has φ2 = -80°, ψ2 = +80°, φ3 = +80°, ψ3 = -80°, and type V′ is its mirror image. Type VI has a cis-proline in position 3; the cis-proline turn was very elegantly demonstrated by Huber and Steigemann () in the refinement of the Bence-Jones protein REI (see Fig. 33b). Type VII has either φ3 near 180° and ψ2 < 60° or else φ3 < 60° and ψ2 near 180°. Type IV is essentially a miscellaneous category, which includes any example with two of the dihedral angles more than 40° away from ideal values for any of the other types.
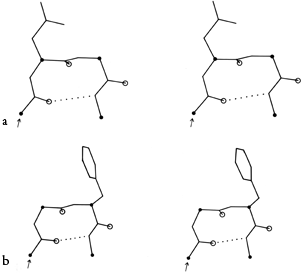
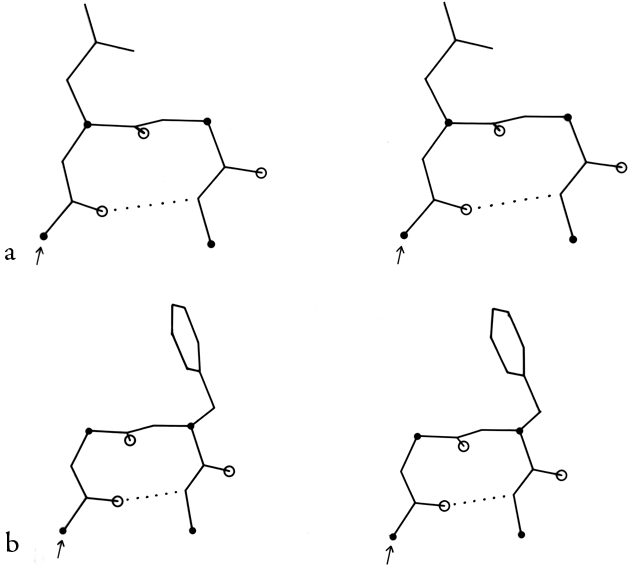
FIG. 32. Stereo drawings of particular examples of types II (a) and II′ (b) turns from the known protein structures. (a) Concanavalin A 43-46 (Gln-Asp-Gly-Lys); (b) carboxypeptidase A 277-280 (Tyr-Gly-Phe-Leu).
FIG. 33. Stereo drawings of particular examples of types VIa (a) and VIb (b) cis-proline turns. (a) Ribonuclease S 91-94 (Lys-Tyr-Pro-Asn); (b) Bence-Jones protein REI 6-9 (Gln-Ser-Pro-Ser).
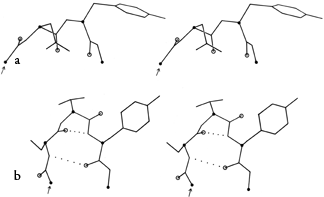
FIG. 34. Stereo drawings of particular examples of type VII (a) and of γ turns (b). (a) Ribonuclease S 23-26 (Ser-Asn-Tyr-Cys); (b) thermolysin 25-27 (Ser-Thr-Tyr).
In order to evaluate the occurrence and distinctness of the major turn types as found empirically in protein structures, Figs. 35 through 37 plot φ,ψ values found for turns in Chou and Fasman (). Figure 35 shows that types I and III form a single tight cluster even for position 3; their ideal φ,ψ values are so close that they could be distinguished only in the most highly refined protein structures. We would suggest eliminating type III as a distinct category.
The ideal values for an inclusive type I category could either be left as they are and would include essentially all the type III examples, or else ψ3 could be changed to about -10° to be closer to the center of the total cluster of values. There is a rather large number of "nonideal" type I turns that occur at the top in Fig. 35b; it might perhaps be productive to group them as type Ib (since their φ3,ψ3 values are in the β region). Some of these turns have an overall "L" shape (similar to Fig. 34a) and some look like a type I turn with the third peptide flipped over.
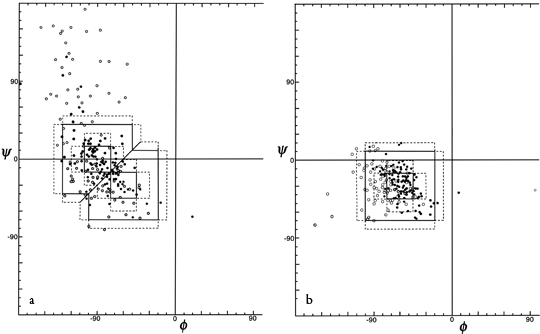
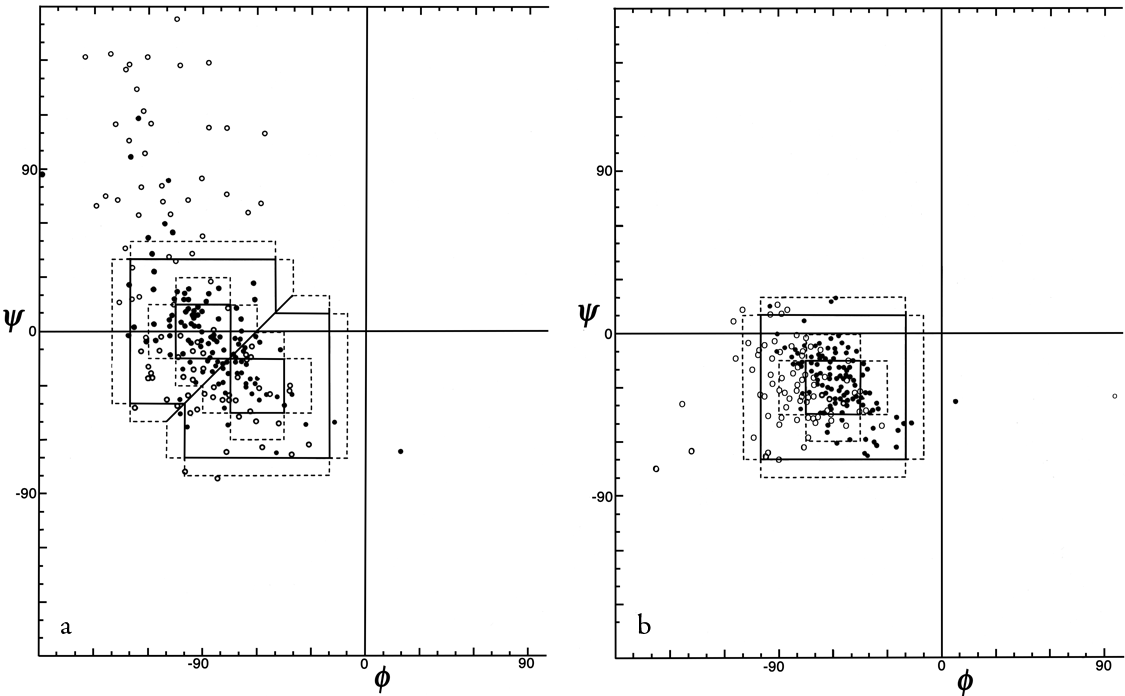
FIG. 35. φ,ψ plots of (a) position 2 and (b) position 3 of empirically observed type I and type III tight turns. In Figs. 35 through 37 the points are plotted from Chou and Fasman (); the outer dotted lines represent the limits of the turn type as defined in that reference and the inner dotted lines represent the limits used in Lewis et al. (); turns with hydrogen bonds are plotted as solid circles and those without as open circles.
Figure 36 shows good clusters for types II and II′ but no evidence of definable type V or V′ examples, which we would also suggest eliminating as separate categories.
Figure 37 plots φ and ψ for the type VI (cis-proline) turns. Although it is a small sample, there is very strong evidence for two distinct conformations which would be considerably easier to distinguish in an electron density map than to tell cis- from trans-proline in the first place. One of the conformations (which could be called type VIa) has approximately α φ,ψ values for the proline, has a "concave" orientation of the middle peptide and the proline ring relative to the overall curve of the turn (see Fig. 33a), and typically is hydrogen-bonded. The other conformation (which includes the original examples found by Huber and could be called type VIb) has approximately β φ,ψ values for the proline, has a "convex" orientation of the middle peptide and the proline ring (see Fig. 33b) and is usually not hydrogen-bonded.
[An additional, even tighter, turn type involving a cis proline has recently been described in Videau et al. (2004); ref ?? called the cisPro touch-turn, it is apparently somewhat strained and is common only at binding and active sites.]
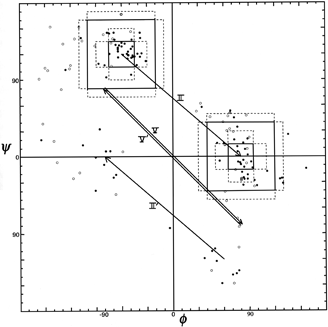
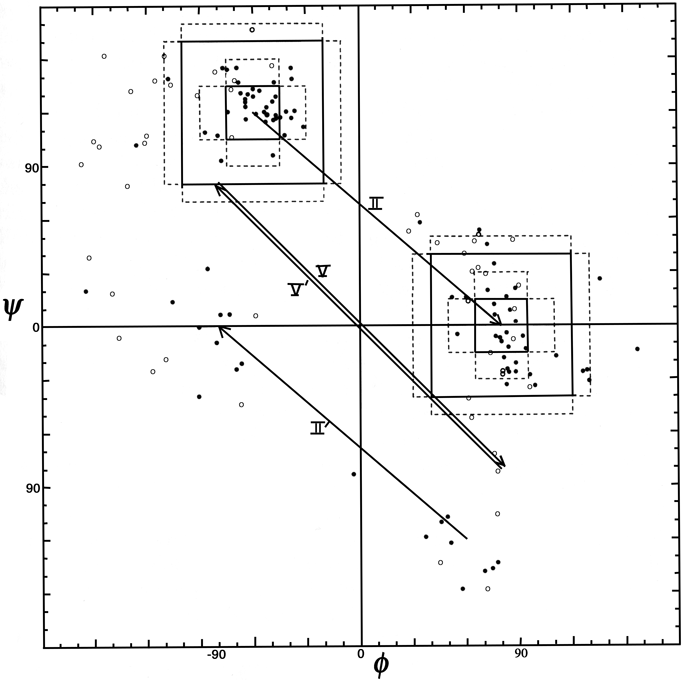
FIG. 36. φ,ψ plot for positions 2 and 3 of tight turns type II, II′, V, and V′. Arrows go from ideal values of position 2 to position 3 for each turn type.
Since type VII turns are defined by only two angles and can have two different values for those, they vary greatly in appearance. Of the nine observed examples at least half are questionable (for instance, staphylococcal nuclease 47-50 is at the end of a partially disordered loop, and for rubredoxin 46-49 the unconstrained refinement has placed the atoms of the middle peptide out of line just enough so that the ordinary definition of φ and ψ is meaningless). Therefore type VII also seems unjustifiable as a distinct category. Some of the type VII turns (and also some type IVs) fall at the edge of the cluster of φ,ψ values seen for type Ib (see above), and perhaps could be included in that group.
In summary, then, tight turns can be rather well described by a set of categories consisting of types I, I′, II, II′, VIa, VIb, and miscellaneous (IV), with the possible addition of type Ib.
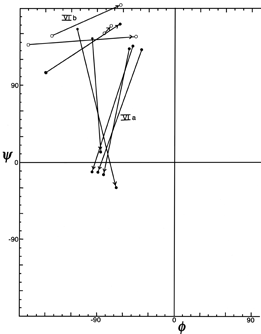
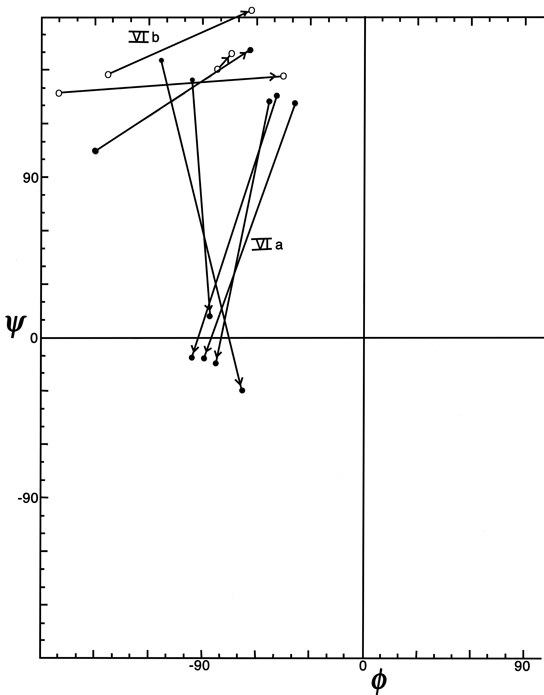
FIG. 37. φ,ψ plot for the cis-proline (type Vl) turns from Chou and Fasman (), plus the two examples in the Bence-Jones protein REI. Arrows point from position 2 to position 3 (the proline) for each example. The two conformational groups are labeled as VIa and VIb.
In order to demonstrate what the various types of turns actually look like, Figs. 31 through 34 show stereo views of turn examples from real structures that have φ,ψ angles very close to the defining values for each type. Type III is illustrated for completeness, but it cannot be distinguished from type I by inspection unless it is part of a continuing 310-helix. Types IV and V are not shown, because type IV is a miscellaneous category and there are no ideal cases of type V (see Fig. 36). The turns are all shown in approximately the same standard orientation: with the mean plane of the four α-carbons in the plane of the page and the chain entering at the lower left. In this orientation the β-carbons are always at or above the plane for types I, I′, II, and II′ turns (since only the backbone conformation can be mirrored). The virtual bond dihedral angle defined by the four α-carbons is close to 0° for type II or II′ and is somewhat positive (averaging about +45°) for type I and somewhat negative for type I′. All four types have the third peptide essentially in the mean α-carbon plane. If the carbonyl oxygens are visible in an electron density map, then these four turn types can be fairly readily distinguished. In types I and II′ the second carbonyl oxygen points approximately 90° down from the plane, while in types II and I′ it points approximately 90° up. The first oxygen points nearly 90° down from the center of the plane in type I, nearly 90° up in type I′, slightly up [ down ] in type II, and slightly down [ up ] in type II′. The position of the second carbonyl oxygen, then, distinguishes between types I and II (or I′ and II′), while the position of the first carbonyl oxygen distinguishes types I vs II′ (or II vs I′). For either distinction intermediate cases should be rare, because they lie in a strongly prohibited region of the φ,ψ map.
The simple conception of a tight turn as approximately planar with a linear hydrogen bond is fairly accurate for type II. However, even an "ideal" type I turn is decidedly nonplanar, with the NH and CO of its hydrogen bond almost perpendicular to each other. That oxygen is in the plane of the last three α-carbons, but the first α-carbon and peptide are swung up out of the plane, producing the 45° virtual dihedral angle.
One additional sort of tight turn involving only three residues has been described theoretically () and also observed at least once in a protein structure (). This is the γ turn, which has a very tight hydrogen bond across a seven-atom ring between the CO of the first residue and the NH of the third (see Fig. 34b). It also can continue with a normal β sheet hydrogen bond between the NH of residue 1 and the CO of residue 3. Residues 1 and 3 are not far from the usual β conformation, while φ2 = 70° and ψ2 = -60°. [The γ turn is real but rare, having a somewhat distorted H-bond and bond angles spread slightly to avoid a clash between Cβ(2) and CO(1). It has been treated in surprisingly disparate ways by different sections of the structural biology community. It is invoked rather too routinely in peptide nmr studies, perhaps influenced by the fact that the γ-turn φ,ψ values (and the mirror-image γ′ at =70°,60°) are the overwhelming global minima for energy calculations in vacuo (e.g. Head-Gordon, 1991), while the γ-turn conformation is avoided when possible by protein crystallographers because that region of the φ,ψ plot is classed as forbidden by Procheck (Laskowski, 1993), the standard structure-validation program. We would recommend an intermediate level of enthusiasm (Lovell, 2003).]
Although the presence of the hydrogen bond led to the initial characterization of tight turns by Venkatachalam (), hydrogen bonding was dropped as a necessary condition as soon as any surveys were done on known protein structures (e.g., ), because numerous examples were found outside plausible hydrogen-bonding distance but with otherwise very turnlike conformation. About half of the turns listed in Chou and Fasman () are hydrogen-bonded (by the criterion that O1 to N4 is less than 3.5 Å). Apparently the various turn conformations are sufficiently favorable so that they do not require stabilization by the hydrogen bond. This should not be surprising, since the turn types essentially consist of the basic α, β, and left-handed glycine conformations in various combinations. Also, since turns typically occur at the surface, peptides can hydrogen bond to solvent when not bonded to each other.
There are a number of characteristic residue preferences for tight turns. The most general is a strong tendency for turn residues to be hydrophilic (e.g., ; ), which might reflect inherent conformational preferences but is more probably a result of the almost universal location of turns at the protein surface where they interrupt or join together segments of secondary structure that are more internal. Glycines are quite common in tight turns, as can be inferred from their preference in types II, I′, and II′; however, glycine is actually not quite as common as would be implied by energy calculations (see ). Proline is also common in turns; besides the cis-proline turn, proline also fits well in position 2 of types I, II, and III turns and position 3 of type II′. About two-thirds of the Pro-Asn and Pro-Gly sequences in the known protein structures are found as the middle two residues of a tight turn ().
Tight turns can combine with other types of structure in a number of ways. In addition to their classic role of joining β strands, they often occur at the ends of α-helices (see Section II,A). A type II turn forms a rather common combination next to a G1 β bulge (see Section II,D). Isogai et al. () have surveyed the occurrence of successive tight turns, which either form approximately helical features or else form more complex chain reversals than single turns.
[As noted above, the most important later insight about tight turns was the demonstration by Sibanda and Thornton () that the classic role at the end of a β-hairpin can be filled well only by the otherwise-rare types I′ and II′, since the virtual dihedral angle formed by types I or II has the wrong handedness to mesh with the right-handed twist of the β-strands in the hairpin. A more recent survey of tight turns can be found in (Wilmot and Thornton, 1988).]
In addition to the approach described at length above, a number of authors have adopted a very useful but much looser approach to defining turns (see ; ; ). Instead of a detailed conformational analysis in terms of conformational angles, hydrogen bonds, etc., these authors want a concept of turns that can be defined systematically and reproducibly from preliminary α-carbon coordinates and that (except for Levitt and Greer) is meant to include also the larger and more open direction changes in the polypeptide chain. Kuntz looks at direction changes for Cαn—Cαn+1 vectors versus Cαn+x—Cαn+x+1 where x is 2 (for usual tight turns) or more; turns have direction changes greater than 90° and short Cαn to Cαn+x distances. Levitt and Greer assign turns to nonhelical, non-β segments for which the virtual dihedral angle defined by four successive α-carbons is between -90° and +90°. Rose and Seltzer define turns as local minima in the radius of curvature calculated from points Cαn-2, Cαn, and Cαn+2, with the modification that turns correspond only to places where the chain in both directions cannot be fitted inside a single rigid cylinder of 5.2Å diameter. Of course, the conformational approach of Lewis et al. () defining detailed turn types must start with a general definition also, which happens to be a Cαn to Cαn+3 distance less than 7Å. Conversely, any of the above general definitions could be used as a starting point from which to examine detailed conformations.
Both of these approaches have their strengths and their limitations. A great many people have deplored the fact that there is not very close agreement between the sets of turns (or of any other structure type) identified by any two different people (or computer programs) for a given protein. Each author suggests that the problem can be solved if everyone else accepts his definitions and criteria. Not only does this seem unlikely to happen, but it would probably be very undesirable. The major reason for the discrepancies is that each author has a different set of purposes for which he wants to use the structural characterization, and each is working from a data base of structures known to widely varying degrees of detail and reliability. Even the standard IUPAC-IUB conventions (1970) recognize two different definitions of α-helix, for instance: one based on φ,ψ values and the other on hydrogen-bonding.
The looser sort of turn definition derived from Cα positions might be the most useful one for studying protein folding and perhaps even for predicting turns. It can be applied to the largest available data base since it requires only α-carbon coordinates. However, in a very real sense it is not appropriate by itself for the accurately determined structures because it is incapable of taking into account the enormous amount of additional information they contain. For example, Levitt and Greer calculate possible hydrogen bonds from just Cα positions, which is a useful way of extending partial information; however, where atomic coordinates are available it turns out that a small but significant fraction of those bonds are definitely not present. Some form of detailed, conformational definition for turns is clearly needed for purposes such as energy calculations, examination of side chain influences, or correlation with spectroscopic observations such as CD or Raman. The detailed definitions will probably be increasingly fruitful as the number of highly refined protein structures increases; one severe problem at present is that they have usually been applied uncritically to all available sets of complete atomic coordinates, regardless of the fact that very few of the structures are known well enough for the distinction of 30° in dihedral angle between types I and III to have much meaning, and that in places where carbonyl oxygens were not visible in the electron density map even the distinction between types I and II is ambiguous. The best solution is probably to continue using whatever turn criteria are most appropriate for a given purpose but to state the criteria explicitly and to give careful consideration to selection of a data base. [These days such classification of structure motifs should always use quality filters based on both resolution and B-factor.]
By any sort of definition, turns are an important feature of protein structure. Kuntz () found 45% of protein backbone in turns or loops; Chou and Fasman () found 32% of protein chain in turns (counting four residues per turn); and Zimmerman and Scheraga () found 24% of the nonhelical residues in turns (counting only the central dipeptide). There are also some particular proteins whose structure appears heavily dependent on turns: Fig. 38 shows high-potential iron protein (), with the 17 turns in 85 residues indicated and their location at the surface evident.
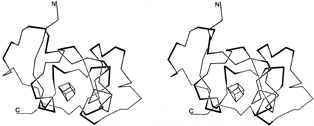
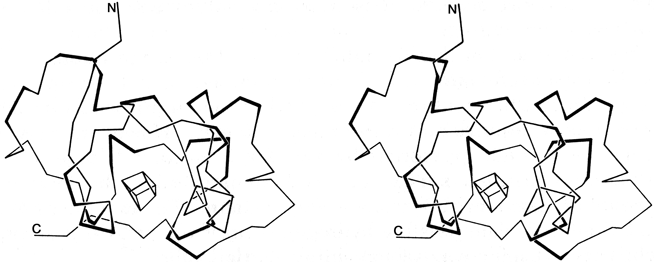
FIG. 38. Stereo drawing of the polypeptide backbone of high-potential iron protein. Tight turns are shown with their central peptide as a dark line. The box in the center represents the iron-sulfur cluster.
Large portions of most protein structures can be described as stretches of secondary structure (helices or β strands) joined by turns, which provide direction change and offset between sequence adjacent pieces of secondary structure. Tight turns work well as α-α and α-β joints, but their neatest application is at a hairpin connection between adjacent antiparallel β strands, where the hydrogen bond of the turn is also one of the β sheet hydrogen bonds, as in Fig. 39. [But see comment above.]
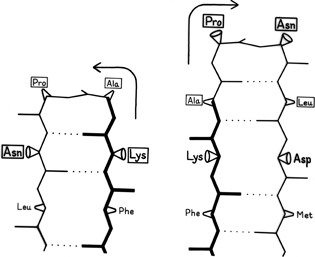
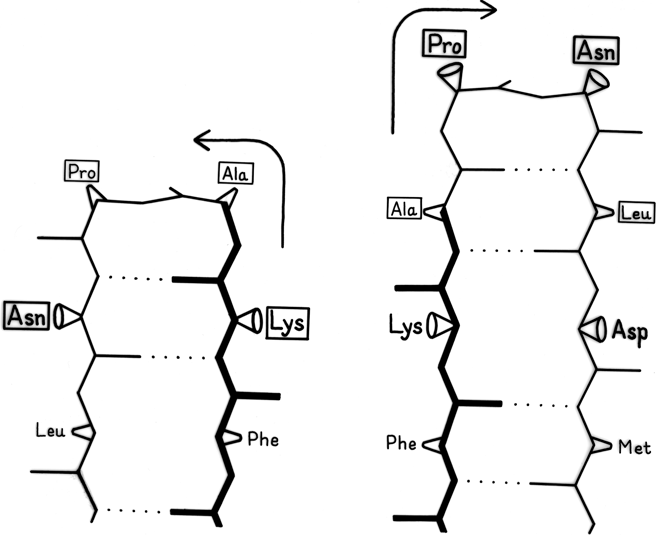
FIG. 39. An example of the effects of shifting the sequence location of a tight turn by one residue. The reference strand Phe-Lys-Ala is in the same position for both cases and is shown in heavy lines; the 4 turn residues are boxed. When the turn is at residues Lys-Ala-Pro-Asn the second β strand must lie to the left of the first, while if the turn is shifted to residues Ala-Pro-Asn-Leu the second β strand must lie to the right of the first. For the sequence illustrated here, the right-hand position would be preferred.
It has often been suggested (e.g., ; ) that turns can provide a decisive influence in directing the process of protein folding to the native conformation, since they seem ideally suited to help specify as well as encourage the decisive long-range interactions that form tertiary structure. As one simple example of the way in which turns can direct and specify other interactions, let us consider what happens when a tight turn immediately joins two adjacent antiparallel strands, as shown in Fig. 39. During the folding process it must be determined whether strand B will lie to the left or to the right of strand A. If the position of the tight turn is shifted by one residue along the sequence, then the turn must be made in the opposite direction to preserve hydrogen-bonding and amino acid handedness, as shown in the two parts of the figure. If the first strand runs from bottom to top and if the side chain in position 1 of the tight turn points toward you, then the second strand must lie to the right; if the side chain in position 1 of the turn points away, then the second strand must lie to the left. Since there are strong positional preferences for the residues in tight turns, it seems plausible that they can actually exert this sort of influence on the folding of neighboring strands.