It has been evident for some time both that a random search through all conformations could not possibly explain protein folding () and also that the structures themselves show evidence of systematic local folding patterns. The consistent presence of domains in the larger proteins strongly suggests that they are folding units (; ), and for some proteins it is known experimentally that an isolated domain can fold spontaneously (e.g., ). A domain usually is made up from a single continuous portion of the backbone; however, the idea of separately folding domains, which then associate to form the intact protein, gains additional support from the frequency with which there occurs a short "tail" or "arm" at one end of a domain sequence which folds over to wrap against the outside of a neighboring domain. Figure 66 shows the structure of papain, which is a classic example of domain-clasping arms. Presumably, the placement of such arms is one of the last events in protein folding, which helps bind together the preformed domains.
It has frequently been pointed out (; ; ; ) that the very high occurrence of associations between secondary-structure elements that are adjacent in the sequence is almost certainly a result of the fact that such nearest-neighbor elements are far more likely to come together during folding. This sort of regularity implies that at least some features of the final protein structure are under fairly strong control by the kinetic requirements of the folding process.
Additional sorts of regularities seen in our general classification of structures allow one to generalize the above idea still further. The prevalence of a few simple patterns of overall topology, and especially such features as the right-handedness of crossover connections and the frequency and handedness of Greek keys, strongly suggest the hypothesis that medium-sized as well as strictly local sections of polypeptide backbone have correlated conformations and tend to fold up as a concerted, interacting unit. One of the most interesting supports for this idea is the difference in statistical distribution of topologies that is seen between antiparallel α, antiparallel β, and parallel α/β structures. The parallel α/β structures are greatly influenced by the relatively long-range regularity of crossover handedness, which together with protection for both sides of the sheet produces the doubly wound α/β structure. In contrast to that situation, three-helix units with the first helix parallel to the third one show no handedness preference whatsoever. Although the possible topologies are exactly equivalent for antiparallel α bundles and for antiparallel β barrels, the frequency with which the various possibilities occur is very different for the two cases. Greek key topologies are about four times as common relative to up-and-down topologies for β structures as compared with α ones; the helical Greek keys occur with either handedness, while 12 of the 13 Greek key β barrels are counterclockwise. Pair associations in the β and α/β structures unambiguously show quite long-range correlations. Such correlations are most easily understood if fairly long portions of the polypeptide chain tend to fold as concerted units, such as the coiling up of a twisted, two-stranded β ribbon shown in Fig. 100. The distribution of features seen in helical proteins is ambiguous: it does not rule out the possibility of long-range concerted folding units, but it does not provide any particular support for such an idea. The observed helical structures could be explained by a simple model in which each new helix-pair association is independent of the topology of earlier pairs.
It has long been assumed that among the fluctuating conformational states early in the protein folding process, local elements of secondary structure are formed for a significant portion of the time, evidence comes from the experimentally observed behavior of synthetic polypeptides (e.g., ), from theoretical calculations of locally determined stability (e.g., ), and even from the degree of success achieved by secondary-structure predictions based only on single-residue, pair, or triplet sequences (e.g., ). Particularly favorable such local regions of structure can act as nucleation sites to start and guide the folding process. Many proposed schemes of folding nucleation single out just one type of structure that seems especially suited for forming the first nuclei. The chief candidates that have been proposed as folding nuclei are α-helices, either alone (; and ) or in combination with β strands (); pairs of β strands brought together by a tight turn (; ) or as long double ribbons (); and hydrophobic clusters (). The proposals for helical nuclei postulate that in predominantly β proteins the helices in the nucleation structures later unfold into extended strands. However, backbone connectivity has its maximum influence early in the folding process, so that topological patterns in the final structure are very sensitive to the order and mechanism of folding, as we have seen before in the contrast between the orderly topology of β strands and the random topology of disulfide connections. Therefore, if nucleation sites are basically similar for all types of structures, that similarity should show up in the overall topological patterns. Instead, as we have seen above, each of the broad types of structure shows characteristically different patterns of pair associations, coiled features, and handedness. Nucleation by hydrophobic clusters is harder to judge from the appearance of the final, folded structures. In proteins with strong long-range regularities of secondary structure it seems very unlikely that the earliest stages of folding are controlled entirely by hydrophobic associations, but there might be pure nucleation by hydrophobic clusters in the more irregular structures.
Judging from the types of regularities seen in the final structures, it seems likely that the typical folding nuclei are different for each of the three largest categories of structure: presumably those nuclei are individual helices and pairs of helices for the antiparallel α structures, β—α—β loops for the parallel α/β group, and two-stranded β ribbons for the antiparallel β structures. The small S—M proteins presumably either nucleate by helices or β ribbons which may be partially lost later or else by hydrophobic clusters. This diversity of folding nuclei would fit fairly well with Rose's "lines and hinges" model () except that different types of lines are not equivalent, and only for the antiparallel α case could they be considered as joined by completely flexible hinges. Tanaka and Scheraga () have also proposed a model with diverse nuclei that are determined by neardiagonal regions of local interaction on the diagonal contact plot which fold by steps rather similar to the ones proposed below, except that forming contacts in rigorous order of increasing separation in the sequence does not permit explanation of any topological regularities larger than pairwise.
One last suggestive feature that is seen in the known protein structures is the frequency with which they "almost match" some prototypical structure. As an example of this sort of deviation, plastocyanin () is an antiparallel β barrel with seven well-formed β strands and an eighth strand which makes only one or two β-type hydrogen bonds, includes a short helix and an irregular excursion, and is slightly displaced from the position for an eighth β strand. If just the seven good β strands are counted as part of the barrel it has an unusual and complicated topology, but if the irregular eighth strand is included the structure is a Greek key barrel of the usual handedness. It may well be that plastocyanin folds as a more regular eight-stranded barrel but effectively loses the β structure in that eighth strand during the final process of adjustment to optimize fit for all the side chains. The significance of the eight-stranded Greek key structure for plastocyanin is reinforced by the fact that the Greek key structure is clearly present in the related protein azurin, with well-formed β structure for that same eighth strand (). There are many other examples of such "approximate" pieces of structure although there is not always a convenient related protein to confirm the assignment. Such features could be explained if proteins first fold to form a maximum amount of regular secondary structure but then may lose some portions of the secondary structure in the final stage of adjusting all interactions for maximum stability. This sort of unfolding and loss of regularity at the final stages has been suggested before on varied sorts of evidence, both for helices (; ) and for β strands (; ). The entire category of S—M proteins is presumably an exaggerated case of this sort of process, in which the amount of adjustment needed to accommodate disulfides or metals into these small proteins is often enough to disrupt the secondary structure almost beyond recognition.
By putting together all of the ideas discussed above, we can propose a speculative general scheme of protein folding as suggested by the properties of the final structures.
The proposed folding process involves four stages, which could be expected to be at least partially separated in time but are not rigorously sequential. Figure 109 illustrates the stages of folding as they might apply to each of the major structure categories. The first stage is the classic one of forming, in a probabilistic and fluctuating sense, individual elements of α-helix, extended strand, or tight turns and of combining two or three of those elements into the first folding nuclei. This does not involve backbone conformations different from those that would be present in a rigorously random coil; it simply involves a difference in the statistics of their distribution in favor of more correlation between the conformations of adjacent residues. Helices have the advantage of hydrogen-bond formation and of cooperativity, and the helices undoubtedly are more regular and can persist for much longer times than isolated, or perhaps even than paired β strands. However, extended strands have the advantage that a much broader range of conformational angles is capable of taking part in β structure, and it could well be that extended strands capable of further interaction are present for about as large a fraction of the time as are individual helices. Once a pair of helices, β—α—β loop, a two-stranded β ribbon, or a large hydrophobic cluster has formed, it would presumably have enough stability to act as a nucleation site for further folding. At least for large domains, it seems unlikely that there is a unique initial folding nucleus, since the relative stability and probability of occurrence would often be similar among, for instance, several possible β—α—β loops. Indeed, the most common topologies are the ones that would permit the most alternative folding pathways ().
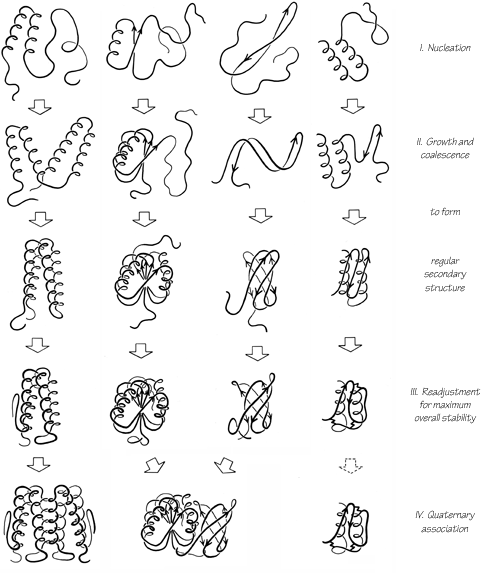
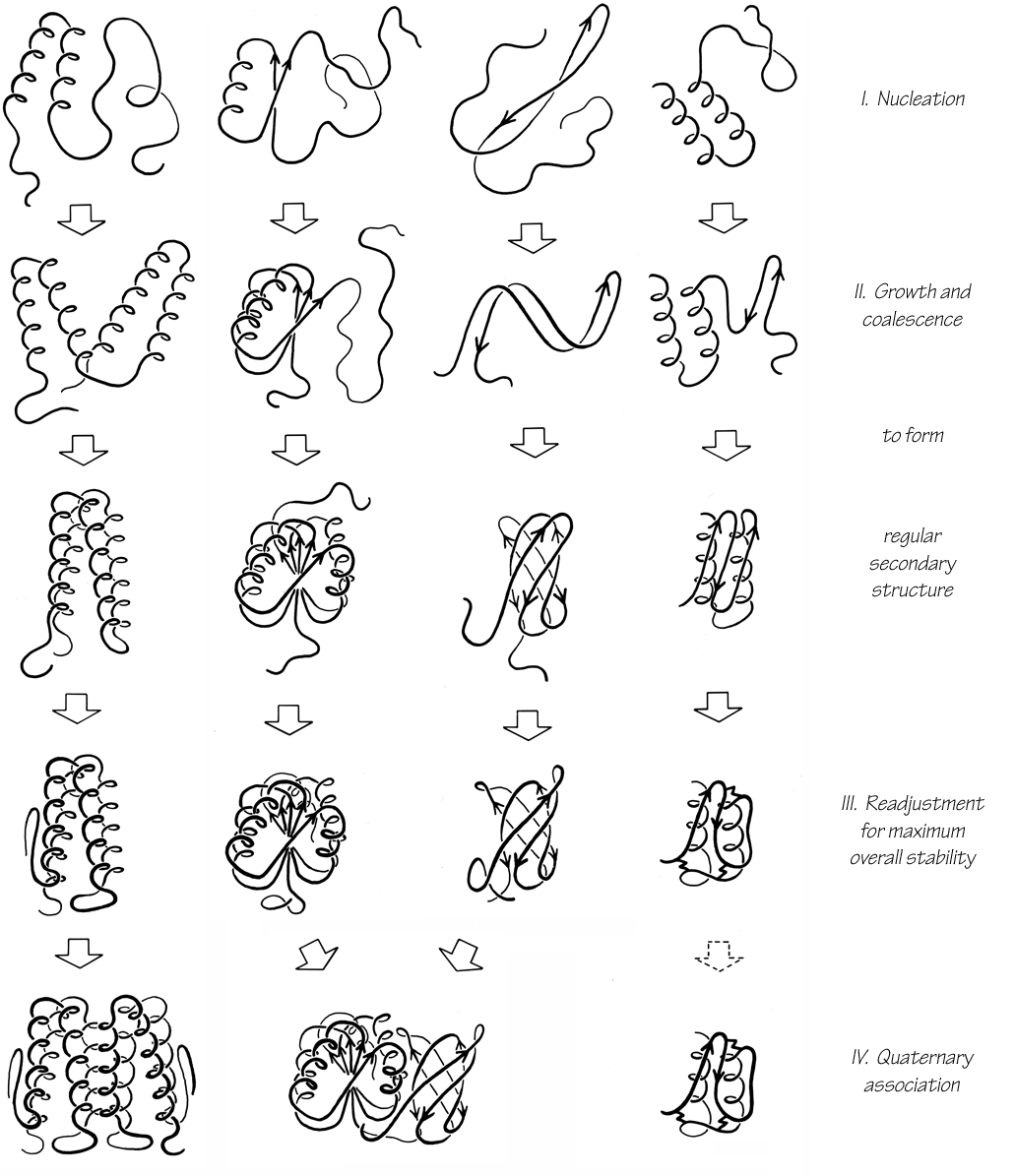
FIG. 109. Possible successive steps in the protein folding process as they might apply to a typical example of each of the four major categories of structure. See text for fuller explanation.
The second stage of folding is the growth and coalescence of secondary-structure elements two or three at a time to form successively larger substructures. The characteristic associations formed at this stage depend on the type and order of secondary-structure elements in the sequence. All-helical structures may associate fairly independently, one nearest-neighbor pair at a time. It is proposed that β—α—β structures fold concertedly by throwing up loops. Antiparallel β structures probably form two-stranded ribbons from nearest-neighbor strands separated by turns; they can then add on strands or pairs of strands to either side of an initial ribbon, or they can coil up a very long ribbon into a Greek key. At the end of this second stage all of the major regular structures are in place, sometimes in a more complete or more regular form than in the final native structure.
The third stage is a process of many readjustments to settle down into a comfortable, stable overall structure. At this stage disulfides are joined in their final native pairing, metals and prosthetic groups are bound, β bulges are formed, and cis-trans isomerization of prolines occurs if necessary (see , ). Side chain conformations are adjusted to provide optimal fit, and some main chain conformations are also adjusted. Occasionally this might produce additional secondary-structure interactions, but it is much more likely to disrupt some of the preexisting secondary structure; mainchain hydrogen-bonding lost at this stage is more than compensated by side chain interactions. This third, readjustment, stage of folding would normally be expected to be very much slower than any of the other steps. For a one-domain, single subunit protein the folding process would then be complete (unless proteolytic cleavages or some other modifications are needed). It may be that the kind of major reshuffling seen during the folding of pancreatic trypsin inhibitor () can be considered as an especially pronounced example of these final readjustments, although the fact that the incorrect intermediates are not very compact suggests that they may represent a rather different process that can happen in addition to the steps considered here. In general, the final structures of the small S—M proteins suggest that they undergo more extensive rearrangement than other proteins.
The fourth stage of folding is the association of domains (and/or subunits). Sometimes association might start at the end of the second stage, but in general it would probably happen only after readjustments within domains were fairly complete. Domains primarily associate as rigid bodies, but there are usually adjustments of side chains at the contact surface, and "arms" that clasp opposite domains cannot old mto their final conformation until this last stage. Association of subunits is equivalent to association of domains, except for the difference in kinetics produced by the covalent attachment.
The most characteristic features of this proposed folding scheme are the proposal of different kinds of nucleation for the different major structure types, the postulation of some rather large-scale concerted folding units, and the prediction of folding intermediates with somewhat greater amounts of the same sort of secondary structure found in the final nahve protein. The last effect might turn out to be most pronounced in those proteins with very irregular secondary structures.
In the final analysis protein folding will be really understood only with the aid of much more extensive, direct experimental evidence. Speculatlve hypotheses can be useful, however, in suggesting potentially fruitful questions for experimental investigation. Probably the most important idea suggested by the above schema is that there are likely to be considerable systematic differences in the kinetics of foldmg between the various major structural categories of proteins.